[2nd_week-day2]미적분
행렬분해(matrix decompositiion)
- LU 분해(LU decomposition)
- QR 분해(QR decomposition)
- 특이값 분해(SVD, Singular Value Decomposition)
LU 분해(LU decomposition)
⇒ 주어진 행렬을 L(Lower triangular), U(Upper triangular) 곱의 형태로 분해(PLU 분해)
역행렬을 통해 해를 구하는 것보다 수치적 안정성이 좋고,
$Ax = b$ 에서 $b$가 변동이 자주 있는 경우가 많다. 이때, 업데이트 마다 해를 실시간으로 구할 수 있음.
*행렬의 곱은 병렬처리(parallel processing)로 가속할 수 있음. (하드웨어 측면이 아닌..)
스칼라 → 벡터 → 행렬
=> 벡터와 행렬은 서로 형태를 바꿀 수 있다.(주로 이미자 처리에서 많이 일어남)
텐서(tensor)는 스칼라, 벡터, 행렬 모두를 아우르는 개념. 숫자가 늘어설 수 있는 방향에 따라 $k$-텐서라고 부름.
- 스칼라 : $0$-텐서
- 벡터 : $1$-텐서
- 행렬 : $2$-텐서

(출처:https://www.google.com/url?sa=i&url=https%3A%2F%2Fascelibrary.org%2Fdoi%2Fabs%2F10.1061%2F%28ASCE%29IS.1943-555X.0000339&psig=AOvVaw0G02tGtNjW9m3r55l0iB8n&ust=1607436937809000&source=images&cd=vfe&ved=0CA0QjhxqFwoTCOCkjqOKvO0CFQAAAAAdAAAAABAD)
그런데 $2$-텐서인 행렬에서 원소들이 각각 벡터로 이루어져 있다면, 그림처럼 3-텐서라고 할 수 있다.
(대표적으로 컬러영상을 $3$-텐서라고 할 수 있음. 원소인 벡터가 $3$-벡터라면 RGB 영상, $4$-벡터라면 RGBA 영상이라고 볼 수 있다.)
$4$-텐서는 무엇이 있을까? 바로 컬러 영상에 시간이 포함된 동영상 형태가 될 것이다.
Partitioned Matrix(분할행렬)

행렬을 조각 단위로 분할하여 분할행렬(partitioned matrix) 또는 블록행렬(block matrix)로 사용할 수 있다.
다양한 형태로 사용이 가능하지만, 보통 열벡터를 많이 사용하므로, 그림에서는 두번째 형태를 가장 많이 사용하게 될 것이다.
선형 조합(linear combination)
$Ax$는 행렬 $A$가 가지고 있는 열벡터의 선형조합이다.
⇒ 벡터들에 대한 가중치 합 ($x_1a_1+x_2a_2+···+x_na_n$)
⇒ 즉, 선형시스템을 선형조합의 관점에서 본다면 벡터 $b$를 만들 수 있는 행렬 $A$에 대한 가중치가 존재 하느냐 로 볼 수 있다.
column space(열공간) : 행렬 $A$의 열벡터들에 대해서 가능한 모든 선형조합의 결과를 모은 집합
Consistent Linear System의 경우, $b∈col(A)$
Inconsistent Linear System의 경우, $b∉col(A)$
좌표계 변환
일반적인 선형시스템 $Ax=b$는 사실 행렬 곱셈의 항등원인 $I$가 곱해져있는 것을 알 수 있다.
$Ax=Ib$ 식의 의미는 $A$ 좌표계($A$의 열벡터들을 )에서의 $x$ 좌표값을 가지는 벡터는 표준 좌표계$(I)$에서의 $b$ 좌표값을 가지는 벡터와 동일하다는 것이다.
$v_1, v_2$ 열벡터를 기저(basis)로 하는 $x, y$ 좌표값의 벡터 = $x$-$y$ 좌표계의 열벡터들을 기저(basis)로 하는 $a, b$ 좌표값의 벡터
선형변환 (Linear Transformation)
함수(function)란?
⇒ 두 집한 간의 매핑룰(mapping rule)
- domain(정의역)
- codomain(공역)
- range(치역)
함수 $f$가 다음 두 조건을 만족하면 선형함수(linear fuction) 이다.
변환(transformation)
입력이 $n$-벡터, 출력이 $m$-벡터인 함수 $T(R^n -> R^m)$
연산자(operator)
$n=m$ 인 경우의 함수 $T(R^n -> R^n)$
변환(transformation)의 경우, $m×n$ 행렬 $A$로 정의할 수 있기 때문에 행렬변환(matrix transformation)이라고 할 수 있다.
또, 행렬변환은 위에서 설명했던 선형함수의 조건 두가지를 만족하기 때문에,
선형변환(linear transformation) 이다.
(행렬은 선형변환의 구현체라고 할 수 있다.)
표준행렬(Standard Matrices)을 이용한 선형변환 코딩
위와 같이 $A$가 $n$-벡터 입력을 받는 경우, $n$-차원 표준 기저벡터를 통해 문제를 해결한다.
구현하고자 하는 기능을 각 표준기저벡터에다가 동작시켜서 얻은 결과 벡터를 각 열에 넣으면($T_A(e_i)$), 행렬변환을 코딩할 수 있다.
예시)
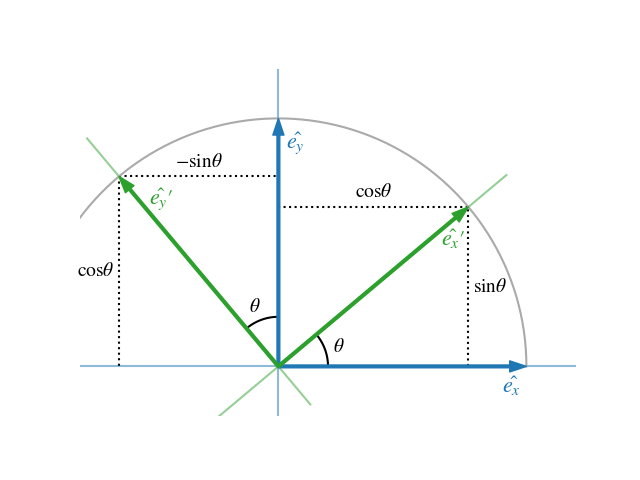
2차원 벡터를 입력으로 받아, 해당 벡터를 반시계방향으로 $\theta$만큼 회전하는 기능을 구현해 보자.
표준기저벡터 $e_1$$(1,0)$을 $\theta$ 만큼 회전시킨 좌표는 $(cos\theta, sin\theta)$ 이기 때문에 $A$의 첫번째 열벡터에 이를 대입하고,
$e_2(0,1)$을 $\theta$ 만큼 회전시킨 좌표는 $(-sin\theta, -cos\theta)$ 이므로 두번째 열벡터에 이를 대입해서 선형변환 $A$를 도출하는 과정은 이와 같다.
 (출처:
(출처: